Tutorial 1 (AY24/25 Sem 1)¶
# Required imports
import sympy as sym
from ma1522 import Matrix
mat = Matrix([[3, 2, -4],
[2, 3, 3],
[5, -3, 1]])
aug = Matrix([3, 15, 14])
aug_mat = mat.row_join(aug)
aug_mat
plu = aug_mat.ref() # Show steps to get to Row Echelon Form
plu.U.rref() # Reduced Row Echelon Form from Upper Triangular Matrix
(b)¶
$$\begin{cases} a &+& b &-& c &-& 2d &=& 0 \\ 2a &+& b &-& c &+& d &=& -2 \\ -a &+& b &-& 3c &+& d &=& 4 \end{cases}$$
mat = Matrix([[1, 1, -1, -2],
[2, 1, -1, 1],
[-1, 1, -3, 1]])
aug = Matrix([0, -2, 4])
aug_mat = mat.row_join(aug)
aug_mat
aug_mat.rref() # Find Reduced Row Echelon Form
mat.solve(aug)[0] # Solve the system of equations represented by the augmented matrix
(c)¶
$$\begin{cases} x &-& 4y &+& 2z &=& -2 \\ x &+& 2y &-& 2z &=& -3 \\ x &-& y && &=& 4 \end{cases}$$
# add aug_pos to specify the position of the augmented column
aug_mat = Matrix([[1, -4, 2, -2],
[1, 2, -2, -3],
[1, -1, 0, 4]], aug_pos = 2)
aug_mat
aug_mat.rref()
mat = aug_mat.select_cols(0, 1, 2) # Remove the augmented column
aug = aug_mat.select_cols(3) # Select the augmented column
# Solve the system of equations represented by the augmented matrix
try:
mat.solve(aug)
except ValueError as e:
print("Error raised due to inconsistent system:", e)
Error raised due to inconsistent system: No solution found for the linear system. The system may be inconsistent.
Question 4¶
Determine the values of $a$ and $b$ so that the linear system
$$\begin{cases} ax && &+& bz &=& 2 \\ ax &+& ay &+& 4z &=& 4 \\ && ay &+& 2z &=& b \end{cases}$$
a, b = sym.symbols('a b') # Define symbolic variables
mat = Matrix([[a, 0, b, 2],
[a, a, 4, 4],
[0, a, 2, b]], aug_pos=2)
mat
plu = mat.ref() # Reduced Row Echelon Form using PLU decomposition
(a)¶
has no solution
# Case 1: b != 2, a = 0
plu.U.subs({a: 0}).rref() # substitute a = 0
(b)¶
has only one solution
# Case 2: b != 2, a != 0
plu.U.rref()
(c)¶
has infinitely many solutions and a general solution has one arbitrary parameter
# Case 3: b = 2, a != 0
plu.U.subs({b: 2}).rref() # substitute b = 2
(d)¶
has infinitely many solutions and a general solution has two arbitrary parameters.
# Case 4: b = 2, a = 0
plu.U.subs({a: 0, b: 2}).rref() # substitute a = 0 and b = 2
Question 6¶
Solve the following system of non-linear equations:
$$\begin{cases} x^2 &-& y^2 &+& 2z^2 &=& 6 \\ 2x^2 &+& 2y^2 &-& 5z^2 &=& 3 \\ 2x^2 &+& 5y^2 &+& z^2 &=& 9 \end{cases}$$
mat = Matrix([[1, -1, 2, 6],
[2, 2, -5, 3],
[2, 5, 1, 9]], aug_pos=2)
mat
mat.rref()
# Alternative Method: Using sym.solve
x, y, z = sym.symbols('x y z') # Define symbolic variables for the solution
vec = Matrix([x**2, y**2, z**2]) # Define a vector of symbolic variables
mat = Matrix([[1, -1, 2],
[2, 2, -5],
[2, 5, 1]])
aug = Matrix([6, 3, 9])
mat, vec, aug
sols = sym.solve(mat @ vec - aug) # Solve the system of equations
for sol in sols:
display(sol) # Print the solutions for each variable
Question 7¶
A network of one-way streets of a downtown section can be represented by the diagram below, with traffic flowing in the direction indicated. The average hourly volume of traffic entering and leaving this section during rush hour is given in the diagram.
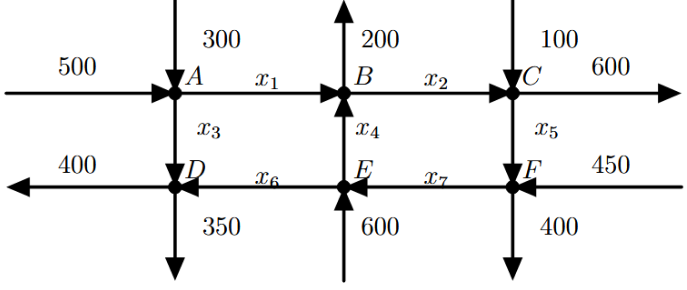
(a)¶
Do we have enough information to find the traffic volumes $x_1$, $x_2$, $x_3$, $x_4$, $x_5$, $x_6$, and $x_7$?
aug_mat = Matrix([[1, 0, 1, 0, 0, 0, 0, 800],
[1, -1, 0, 1, 0, 0, 0, 200],
[0, 1, 0, 0, -1, 0, 0, 500],
[0, 0, 1, 0, 0, 1, 0, 750],
[0, 0, 0, -1, 0, -1, 1, -600],
[0, 0, 0, 0, 1, 0, -1, -50]], aug_pos=6)
aug_mat
aug_mat.rref()
mat = aug_mat.select_cols(*range(7))
aug = aug_mat.select_cols(7)
sol = mat.solve(aug)[0]
sol
(b)¶
Suppose $x_6 = 50$ and $x_7 = 100$. What is $x_1$, $x_2$, $x_3$, $x_4$, and $x_5$?
y = sol[5]
z = sol[6]
sol.subs({y: 50, z: 100}) # Substitute y and z with specified values
(c)¶
Can the road between junction A and B be closed for construction while still keeping the traffic flowing in the same directions on the other streets? Explain.
sol.subs({y: -50}) # Set sol[0] = 0